Dichotomy Paradox(Zeno's Paradox)

What is Dichotomy Paradox?
This paradox is thought to be proposed originally by a Greek philosopher Zeno. Which means that if supposes one has to move from point A to point B such that the distance between the two points is 1 kilometre, then first, the person would have to cover half of the total distance(0.5 km). On reaching 0.5km from A towards B, the person will at some moment cover half of the remaining distance such that the distance between him and point B is 0.25 km. Now, the person again will have to cover half of the remaining distance before reaching point B and this continues for infinite number of times.


Logical thinking-
Initially when one thinks about the dichotomy paradox, one is not able to realize that it is a paradox. The logical thinking that makes it a paradox is that if before reaching the goal one must cover half of each of the distances remaining between him and his destination and the division of the remaining length into half can be infinite number of times then it should be impossible for the person to reach his destination ever, as infinite number of distances must take infinite number of time to cover. But we all know that’s not true, right?

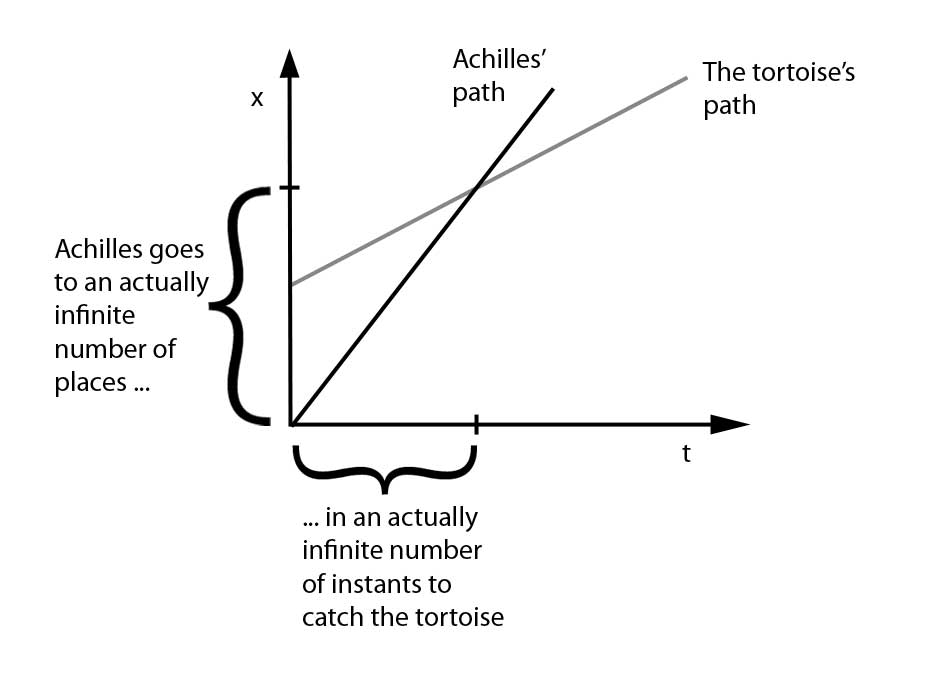
Another situation- A similar problem can be related to dichotomy paradox. Imagine if a person(say Achilles) and a tortoise were to race. The finish line is set at a certain distance and since the tortoise is slower it is given an advantage that it shall start from a point that is ahead of the person’s starting point by a certain distance. What zeno thought about this problem is that when the race starts, the person must first take some time to reach the point from where the tortoise had started the race, but by then tortoise would have moved forward by some distance. Now the person must first cover this distance and when he reaches the point where tortoise was when he reached tortoise’s starting point, the tortoise would have further covered some distance and this continues till infinity. The logical conclusion that comes out here is that at no point of time the person would be able to overtake the tortoise. But in reality we know that is not true.

Dichotomy paradox is not actually a paradox, but it is actually flaw about how we think about things. The thing that leads one to believe that it is a paradox is our interpretation of infinity. In mathematics it is seen that sum of infinite farctions is not always infinite but it can be finite as well. If we take the problem where the person had to go from point A to point B and analyse it mathematically, no matter how many times the distance gets divided in half, the result will always be finite.
D = Sum of half each of the remaining distances the person covers.
Multiplying both sides by 2.
2D= 1+ 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + …….. ∞
Using Eq1, we get,
2D= 1+ D
D=1
With the above proof it is clear that the sum of an infinite series can be finite.
As Hermann Weyl stated that Zeno assumed that between any two points in space there is always another point, without this assumption there is only finite distance between two points, hence there is no infinite sequence of movements and the paradox is resolved.
What other thing that one misses while thinking about such problems is the idea of smallest distance possible between two objects in the universe. This smallest possible distance is called the Planck Length(ℓ P ). It is a unit of length that is the distance light in a perfect vaccum travels in one unit of Planck time. It is equal to 1.616255(18)×10−35 m. In the first problem when the distance between the person and point B becomes equal to planck length, it cannot be further divided in half and thus the person reaches his destination. Similarly in the race problem when the distance between the person and tortoise becomes equal to planck’s length the person overtakes the tortoise and wins the race.

What other thing that one misses while thinking about such problems is the idea of smallest distance possible between two objects in the universe. This smallest possible distance is called the Planck Length(ℓ P ). It is a unit of length that is the distance light in a perfect vaccum travels in one unit of Planck time. It is equal to 1.616255(18)×10−35 m. In the first problem when the distance between the person and point B becomes equal to planck length, it cannot be further divided in half and thus the person reaches his destination. Similarly in the race problem when the distance between the person and tortoise becomes equal to planck’s length the person overtakes the tortoise and wins the race.

Comments
Post a Comment